


Light and its nature have caused a lot of ink to flow during these last decades. Its dual behavior which is known as the Wave-Particle Duality is partly explained by Double-slit experiment of Thomas Young - the observation of interference effects in the Double-slit experiment of Thomas Young definitively show the presence of overlapping waves and he represents the photon motion as a wave - and also by the Photoelectric effect in which the photon is considered as a particle. The photoelectric effect refers to what happens when a material which absorbed electromagnetic radiation emits electrons. However, Einstein himself writes: "It seems as though we must use sometimes the one theory and sometimes the other, while at times we may use either. We are faced with a new kind of difficulty."
SALEH THEORY solves this ambiguity and this difficulty by presenting a three-dimensional trajectory for the photon motion and a new formula to calculate its energy.
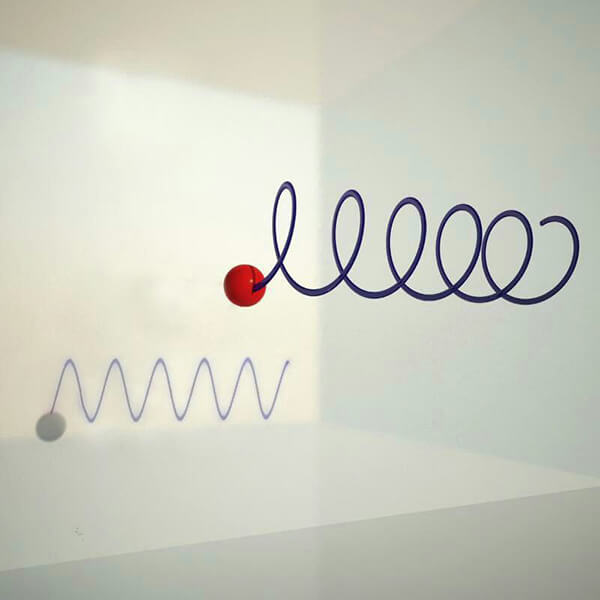
New definition of photon motion
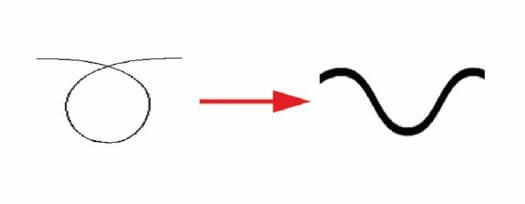
The emission of the photon, following the change in energy level of electron (Fig. 1), causes a motion, which rotates along and around a straight axis at light speed (c): a three-dimensional trajectory combining the both of rectilinear and orbital trajectories. However, the side view of the movement shows still a sine wave. (Fig. 2)
If we imagine the electron as a rotating fountain that turns around itself (Fig. 3), it diffuses the photon in the same way that the fountain projects the drop of water, and the photon will follow the electron rotation over its nucleus. As a consequence, the photon, besides its linear trajectory, it also turns around an assumed axis and ultimately creates a three-dimensional trajectory. To have a little understanding of this, we could take the example of a released spring. That’s to say, this trajectory is a result of the combination of two motions: the rectilinear one and perpendicular circulation around the same axis.

Actually, due to the intensity of energy freed during the emission, photon turns around itself (like the Earth's rotation), and around an assumed axis (annual motion of the Earth) while continuing his rectilinear trajectory.
So one turn of photon's rotation around the assumed axis is equal to the wavelength of a sinusoidal wave.
Thus, the number of turns of the photon in a second have to be consider the Frequency similar to the Planck Formula ( E = h9 ).
Assume now that v→ is the rectilinear speed of photon and ω→ the orbital one (Fig. 4); the photon energy (E), should be calculate according to Newton’s laws and the addition of two vectors:
Ep = kmp v2
Which v is the vector addition of rectilinear and orbital speed:
Ep = mp ( kv2 + k'ω2 )
W = rω

Also ω→ represent the orbital speed and the shape of orbit, could be a circle or an ellipse. So ω→ may have different values.
This leads us to realize that in addition to the Planck formula, we can apply the Newtonian Laws to calculate the photonic energy and, this made, we could have more significant and more coherent notion concerning the behavior of the photon and his movements.
With regard to all factors involved in photonic energy, we represent a new formula:
Guided by this theory, we can establish a complete three-dimensional vision of photon motion, which is justified by Wave–Particle Duality and Newtonian Laws.