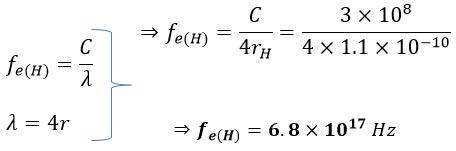A New Method for Fission of Atoms of Elements Using the Resonance Phenomenon 2024

1. The Calculation of the Frequency of Electrons and Nucleus of Atoms

According to the previous articles, electrons of atoms traverse in their specific, continuous, and closed orbits at speeds close to the speed of light. The nuclei of atoms also rotate around themselves at a speed close to the speed of light.

1.1. Calculating the Frequency of Electron of Hydrogen Atom

Given the helical path of electron motion around the nucleus, the frequency of its motion can be determined using the following equations and a straightforward method:

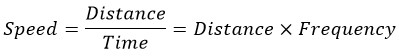
So, in general, it can be said:

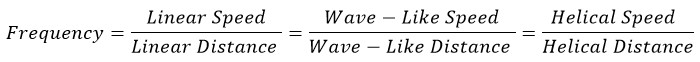
Therefore, the frequency of a single electron in a hydrogen atom can be calculated as follows:

In this context, 𝛌 represents the wavelength, C is the speed of light, and f_e(H) denotes the frequency of the electron in the hydrogen atom. The parameter rH, equivalent to the radius, corresponds to the atomic radius of hydrogen. As another illustrative example, let's calculate the electron frequency for the outermost layer of a Gold atom:

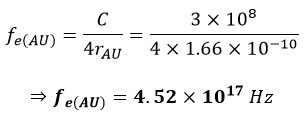
Calculating the Frequency of Proton of Hydrogen Atom

It is quite clear that the Moon orbits around itself and around the Earth, which is itself rotating around its axis and around the Sun. The Sun, in turn, orbits around itself and around the central black hole of the Milky Way galaxy. The black hole is also in a state of rotation. Additionally, electrons orbit around themselves and around the nuclei of atoms. The nuclei, too, rotate around themselves at the speed of light. Therefore, one can write a repeatable sinusoidal equation for the rotation of a proton around itself:

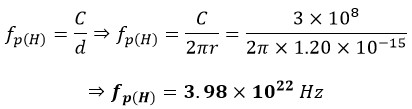
In which r is the radius, and f_p(H) is the frequency of proton of the hydrogen atom. Now, let's proceed to calculate the frequency of the atomic nucleus of Gold Gold f_p(AU):

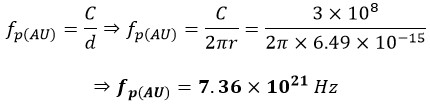
Considering that electrons and nuclei of atoms have specific frequencies in their repetitive motion, and the phenomenon of resonance in nature, it is possible to disrupt the order and coordination of their motion with a laser that has the same frequency as the corresponding electron or nucleus of that atom, leading to fission of the nucleus of the atom.

2. Design and Manufacture of Gravitational and Electron Lasers to Bombard Atoms

Consider the frequency of a specific electron or nucleus of a specific atom to be F1, if we design a laser with the same frequency F1 and emit to that atom, the resonance phenomenon will occur, resulting in fission. According to equations (C = λF or C = λ/T) the same frequencies mean having the same wavelength and equality of the rotational radius of the photons of the laser and the electron or nucleus of the atom.

If the laser has the same frequency as a specific electron in an atom (meaning it has the same wavelength or rotational radius R_mom), they could collide at a specific point. If the frequencies differ, the probability of collision decreases, and it may not occur at all. This is because a photon traverses in a helical path similar to a spring. When these photons are shaped into a laser, it is like an array of photons with a specific and defined radius traversing along a helical path, essentially creating a cylindrical shell.

If the radius of the inner cavity of this cylindrical shell does not match the rotational radius of the electron or nucleus of the atom, either no collision will occur or the probability of collision will be extremely low. The bombarded particles will pass through the central empty space or tunnel without collision. In reality, the optimal laser effect is achieved when the particular laser particles and the electron or nuclear particles have the same rotational radius (same frequency).

Given these explanations and the frequency values of electrons and nuclei, we must manufacture a specific laser to achieve the desired fission from the collision of the laser and the atom.

Note: Given the extremely high difference between the rotational radius of electrons (and nuclei) of atoms and the rotational radius of visible lasers, these types of lasers are not suitable for the fission of an atom. We need to develop a laser with a frequency of at least 10¹⁸ Hz, as common lasers are not applicable. For the fission of a nucleus using this method, we propose using gravitational lasers or electron lasers.