Everything About Universal Constants and their Secrets

One of the most wonderful enigmas in physics is the existence of fixed coefficients and values that appear in various formulas and equations. For instance, consider the famous number "π" in the equations for the circumference and area of a circle, the Planck constant in Planck's quantum energy equation, or the Hubble constant, which relates to the expansion of the cosmos. The fundamental question is: why do such fixed numbers exist in our universe? And what secret lies within their stability and permanence?

The first point is that within any physical system, there is a specific structure, a particular trajectory of motion, and a defined mass, whose value remains constant within that system's framework. For example, if we consider the Moon's orbit around the Earth, the time for one complete revolution can be calculated with remarkable accuracy, with an error of less than a second. This astonishing precision is due to the stability of parameters such as mass, distance, and velocity within that system.

When examining the physical laws expressed as mathematical formulas, we see that all these equations are based on fundamental definitions such as mass, velocity, acceleration, and energy. Essentially, all these relationships stem from the inherent stability of certain key parameters. In systems that display repetitive behaviour, the values of these parameters also stay constant over time. As a result, the ratios between these values remain constant, which we recognise as universal constants.

For example, in Hubble's Law, the velocity of any galaxy relative to us is the product of the Hubble constant (H) and the distance of that galaxy from us:

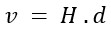
Although the distance between galaxies increases over time, this increase is accompanied by a proportional velocity, such that the ratio between velocity and distance always remains constant. This characteristic gives rise to the constant known as the Hubble constant.

Broadly speaking, universal constants can be considered as ratios between quantities like energy, velocity, or acceleration, and quantities like mass, time, and distance. To put it more simply, if we were to provide a mathematical definition of a universal constant, we could write:

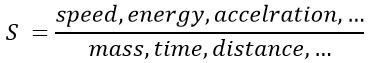
In this equation, S represents a universal constant that is obtained by dividing one or more constant physical parameters (such as energy or velocity) by dimensions like mass, time, or distance.

For example, consider the equation for gravitational potential energy:

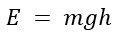
In this equation, if the mass, height, and energy are constant for a specific mass along a specific path, g can be defined as follows:

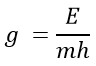
Since E, m, and h have a constant value within a given system, the value of g appears as a universal constant.

Thus, it can be said that universal constants are ratios of stable parameters of nature that appear in physical equations and have emerged from the precise order of the cosmos.

References:

[1] Saleh, Gh. " A New Explanation for the Existence of Universal Constants (G, h, H, ...) in the Universe 2025." Saleh Theory, 27 Feb. 2025, https://saleh-theory.com/article/a-new-explanation-for-the-existence-of-universal-constants-g-h-h-in-the-universe-2025

[2] Saleh, Gh. "New Points about Time and Space." APS April Meeting Abstracts. Vol. 2023. 2023.

[3] Saleh, Gh. "New Discoveries About Gravity?!!! 2." Saleh Theory, 12 Dec. 2021, https://saleh-theory.com/article/new-discoveries-about-gravity-2