
New Discoveries about the Source of Dark Energy, Its Nature, and More: Based on the Initial Energy of the Universe (Big Bang), Hubble's Law, and Its Governing Mathematical and Physical Equations (2025)
Let's consider the Big Bang phenomenon, where a vast amount of energy is released in a minimal volume at a single moment (the Big Explosion), two primary motions can be identified for this explosion:
1. Linear motion with a decreasing linear velocity (Vl→)
2. Rotational motion with an increasing tangential velocity (Vr→)
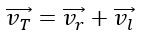
The linear motion arises from an explosion in which a large amount of energy is released at an initial time. In this linear trajectory, acceleration is negative, and over time, the distance from the center (r) increases, but the linear speed decreases (similar to the explosion of a grenade, where the fragments do not extend to infinity). This is because we had an initial explosion, and thereafter no additional energy enters the system in the linear direction. In fact, the most reasonable motion for a simple explosive movement along the linear path is one in which the speed of particles decreases over time as the distance increases:
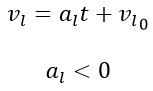
where "vl0" is the initial linear speed.
Now, consider the rotational motion. As we have previously demonstrated, Hubble's Law indicates tangential speed, and the equations for rotational motion are as follows:
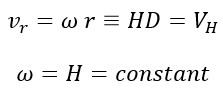
When we observe around us, we see celestial objects like the Moon and the Sun, which we see daily, and the Earth that we stand on, all of which revolve around their respective orbits. Thus, the most evident motion in the universe is rotational motion. In fact, these three visible celestial objects are constantly rotating and follow closed curved paths. It can be said that all celestial objects, from the smallest to the largest, including the Universe itself, exhibit rotational motion, and with the help of Hubble's Law, we can easily determine the tangential speed of more distant objects.
Furthermore, according to the principle of energy conservation, energy neither ceases to exist nor is created; rather, it is merely transformed from one state to another, and the total amount remains constant at any given time. So:
Total Energy at the moment of the Big Bang (ET) is equal to the Rotational Energy (Er) plus the linear Energy (El)
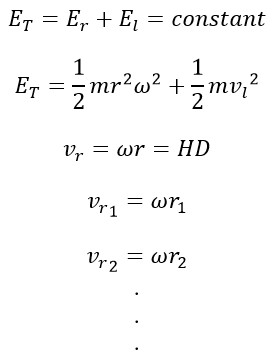
As time progresses, with the presence of linear motion, the radius of the Universe changes, and (r) continually increases (representing the expansion of the Universe). Therefore, we have:
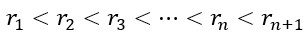
From the above relations, it follows that:
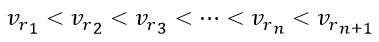
Thus, the tangential acceleration can be derived from the following equation:
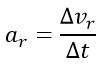
Given the above relations, the tangential acceleration leads to an increase in tangential speed. Since the total energy at the moment of Big Bang or the same total energy (rotational energy + linear energy) remains constant (as confirmed by the conservation of energy principle), the amount added to the rotational energy is equal to the amount reduced from the linear energy.
Result:
Since scientists had previously considered only linear motion and neglected rotational motion when modelling the universe, they were faced with the observation that the speed of celestial objects increases over time, and the farther these objects are from us, the faster they move away (as described by Hubble's Law). In response to this, they sought a "missing energy" to account for the increasing velocities over time, which they called dark energy. Dark energy was proposed to explain the observed acceleration in the expansion of the universe. However, by considering the presence of rotational motion alongside linear motion, and demonstrating that Hubble's Law actually describes tangential speed, it can be argued that dark energy represents the previously unaccounted-for rotational energy. As linear energy decreases over time, the contribution of rotational energy becomes more prominent. In fact, we can propose that dark energy is simply this rotational energy, which becomes increasingly significant as linear energy diminishes.
Dark Energy is equal to the total energy at the moment of the Big Bang minus the linear energy which is equal to the same rotational energy (that was neglected)

References:
 Download PDF
Download PDF 

