
New Discoveries about Hubble's Law
1. The justification of the sphericity and the rotation of the Universe by Hubble's law
If we assume that the Universe is spherical and in addition to increasing its radius, it also has a rotational motion around its axis, its velocity equations can be written as follows:
Total Velocity of Universe = Linear Velocity + Rotational Velocity
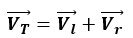
1.1. Linear velocity(V→l):
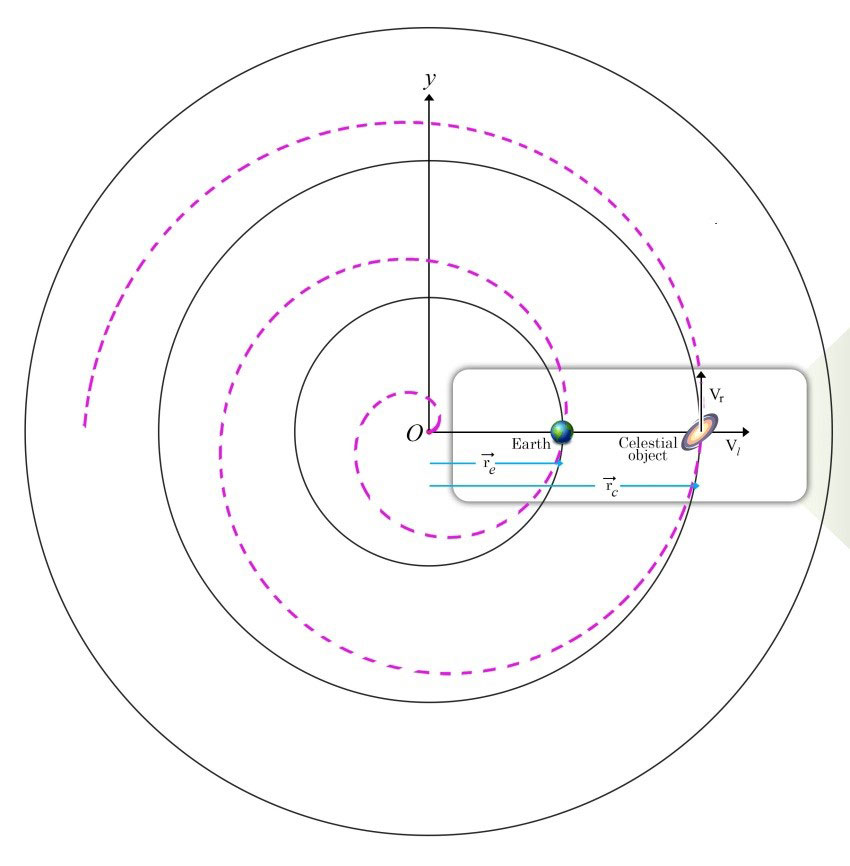
After the Big Bang, all the Universe particles have been released by the initial energy and ejected in a projectile motion. In other words, due to the projectile motion of the Big Bang, an initial energy have been given to the particles and they have been ejected at a very high speed and after billions of years or at the same time the homogeneity of the Universe, they have reached a relative equilibrium and after it, have continued to move at a constant speed “L” and now have the same constant value:
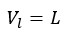
1.2. Rotational velocity(V→r):
At the moment of Big Bang, there was another type of motion, namely rotational motion. In this motion, the rotational velocity depends on two parameters: angular velocity(ω)and rotational radius(r):
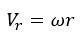
However, due to the nature of the initial projectile motion of the particles, they had also an initial rotational speed and over time and after the Universe became homogeneous, their angular velocity(ω) became constant. In fact, it can be said that after the Universe homogeneity, that is the same relative calm, balance, harmony, uniformity … of the universe, the rotational motion has also got a uniform angular velocity(ω).
But the Universe is expanding at a constant linear velocity and over time the radius of the Universe, simply put, rotational radius(r), increases. So, in fact, our rotational velocity(V→r), which is affected by both the angular velocity parameter(ω) and the rotational radius(𝑟), increases without any force being applied to it. So the general calculation relation of the Universe velocity can be simplified as follows:
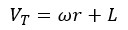
Hubble's law, on the other hand, describes the velocity of a galaxy in the Universe, and the general calculation relation is as follows:
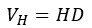
Now we calculate the velocity of the Universe for a galaxy and correspond it to the velocity in Hubble's law:
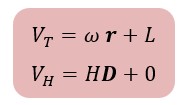
Comparing the above two formulas, it is clear that dimension of "D" is equal to dimension of "r" and dimension of "H" is equal to dimension of "ω". In fact, we can say that "D" is the same "r" that has the length dimension and "H" is the same "ω" that both have time inverse dimension. And since the value of the linear velocity is constant, the linear velocity of the galaxy, in the formula obtained by Hubble, is zero relative to the Milky Way galaxy.
1.3. Calculation method of the Hubble Constant:
The method of calculating the Hubble’s constant is that the slope of the velocity-location diagram of the observed galaxies is considered as the Hubble’s constant. Therefore, the relation can be written as follows:
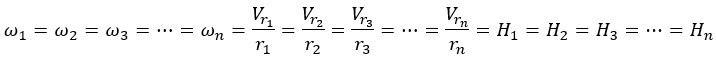
According to Hubble's experimental law VH = HD and the Hubble’s constant calculation method, for galaxies which their linear velocities are in the same direction and therefore their linear velocities relative to each other are zero, the value of (H) is equal to their angular velocity (H) or the same (ω).

Notice:
Based on the above relations and explanations, it can be said that Hubble's law calculates the rotational velocity of galaxies around the center of the Universe and also proves that the Universe is spherical and rotates.
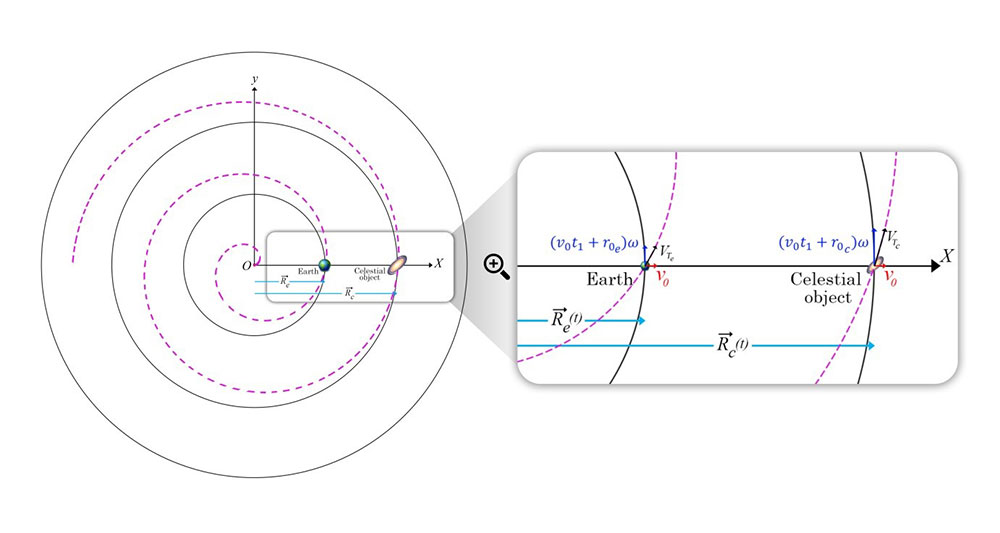
2. The calculation of the real radius of the Universe and its actual rotational velocity by Hubble's law
The Big Bang energy can be calculated by the Monte Carlo Techniques:

For further considerations, we consider the total energy equal to 10110j. So we can write the following relations:
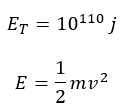
Where “m” is the total mass of the universe and it equals to 1053kg. So we have:
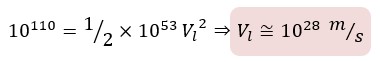
Therefore, the linear velocity of the Universe is about 1028m/s. On the other hand, the lifespan of the Universe is 14 billion years. So we can write:
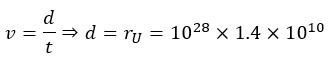
If we change the year to second we have:
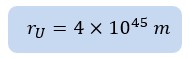
As a result, the current radius of the Universe (rU) is about 1045 meters. If we use the Hubble’s law that gives us the rotational velocity of the Universe, the rotational velocity at the edges of the Universe should be about:
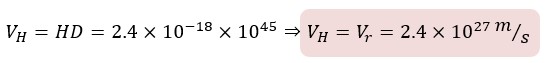
Comparing the linear and rotational velocity of the Universe with the speed of light (C = 3 × 108m/s), we would see that the linear and rotational speeds of the Universe are now more than 1018 times of the speed of light:
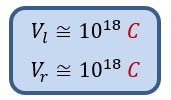
Articles




